פונקציית SIN Excel היא פונקציה טריגונומטרית מובנית ב- excel המשמשת לחישוב ערך הסינוס של המספר הנתון או במונחים של טריגונומטריה את ערך הסינוס של זווית נתונה, כאן הזווית היא מספר ב- excel ופונקציה זו לוקחת רק טיעון יחיד שהוא מספר הקלט שסופק.
פונקציית SIN ב- Excel
פונקציית SIN ב- Excel מחשבת את Sine של זווית שאנו מציינים. SIN בפונקציית Excel מסווג כפונקציה מתמטיקה / טריגונומטריה ב- Excel. SIN ב- excel מחזיר תמיד ערך מספרי.
במתמטיקה וטריגונומטריה, ה- SINE הוא פונקציה טריגונומטרית של זווית, אשר במשולש ישר זווית שווה לאורכו של הצד הנגדי (הצד הזווית הישרה), חלקי אורך ההיפוטנוזה, ומיוצג כ :
חטא Θ = צד הנגדי / היפוטנוזה
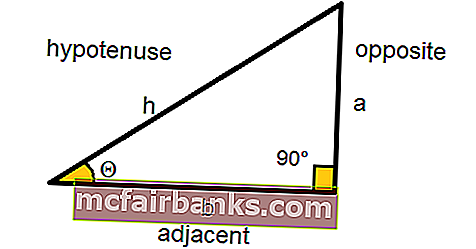
חטא Θ = a / h
נוסחת SIN באקסל
להלן נוסחת SIN ב- Excel.

איפה המספר הוא טיעון המועבר לנוסחת ה- SIN ברדיאנים.
אם נעביר את הזווית ישירות ל- SIN בפונקציית excel, היא לא תזהה כטיעון תקף. לדוגמא, אם אנו מעבירים 30 ° כארגומנט לפונקציה SIN זו באקסל זה לא יזהה כארגומנט חוקי. Excel יציג הודעת שגיאה.
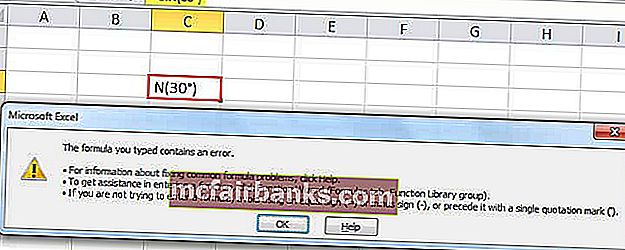
מכאן, שהטיעון שעלינו להעביר חייב להיות ברדיאנים.
להמרת זווית ברדיאן ישנן שתי שיטות
- השתמש בפונקציה המובנית של RADIANS של Excel. פונקציית RADIANS ממירה את המעלות לערך רדיאן.
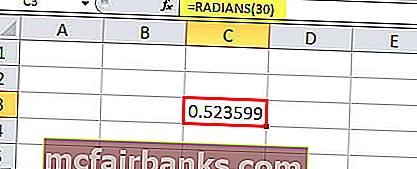
לדוגמא, כדי להמיר 30 ° לרדיאן נשתמש בפונקציה זו, זה לוקח את התואר כמספר, זה יהיה 30 ° כ 30.
= RADIANS (30) ייתן לרדיאן 0.52
- במקרה השני אנו יכולים להשתמש בנוסחה המתמטית להמרת תואר לרדיאן. הנוסחה היא
רדיאן = מעלות * (π / 180) (π = 3.14)
ב- Excel יש גם פונקציה שמחזירה את הערך של Pi, מדויקת ל- 15 ספרות, והפונקציה היא PI ()
לכן, לצורך המרת תואר לרדיאן, נשתמש בנוסחה
רדיאן = מעלות * (PI () / 180)
כיצד להשתמש בפונקציית SIN ב- Excel?
פונקציית SIN ב- Excel פשוטה מאוד וקלה לשימוש. בואו להבין את העבודה של SIN ב- Excel על ידי כמה דוגמאות.
אתה יכול להוריד SIN זה בתבנית Excel כאן - SIN בתבנית ExcelSIN ב- Excel דוגמה מס '1
חישוב ערך סינוס באמצעות פונקציית SIN ב- Excel ופונקצית RADIANS ב- Excel


חישוב ערך סינוס באמצעות פונקציית SIN בפונקציה Excel ו- PI


לתפקוד סינוס ב- Excel יש יישומים רבים בחיים האמיתיים; הוא נמצא בשימוש נרחב בארכיטקטורות לחישוב הגבהים והאורכים של דמויות גיאומטריות. הוא משמש גם ב- GPS, אופטיקה, חישוב מסלולים, כדי למצוא את המסלול הקצר ביותר על סמך מיקום גיאוגרפי של קו רוחב ואורך, שידורי רדיו וכו '. אפילו גל אלקטרומגנטי מתואר כגרף של תפקוד סינוס וקוסינוס.
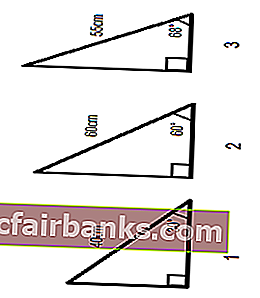
נניח שיש לנו שלושה משולשים ישרים, שניתנים בזוויות ובאורך של צד אחד ועלינו לחשב את אורך שני הצדדים האחרים.
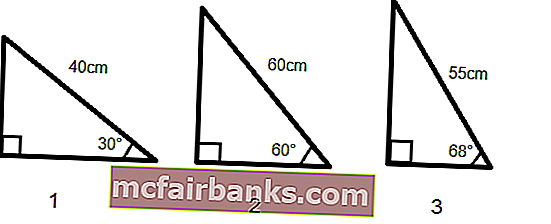


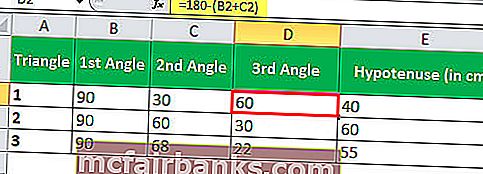
סכום כל הזוויות במשולש שווה ל- 180 מעלות, לכן נוכל לחשב בקלות את הזווית השלישית.
אנו יודעים, חטא Θ = הפוך / היפוטנוזה
אז, אורך הצד ההפוך יהיה Sin Θ * hypotenuse
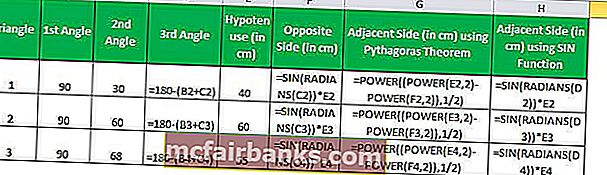
ב- Excel, האורך של הצד הנגדי (הצד הניצב) יחושב על ידי הנוסחה SIN
= SIN (RADIANS (C2)) * E2
יישום נוסחת ה- SIN שניתנה לעיל לשלושה משולשים נוכל לקבל את אורך הניצב של המשולשים.
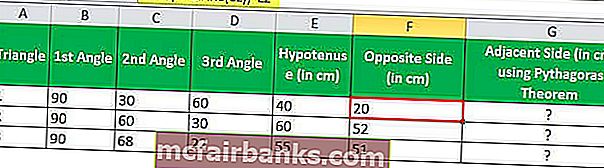
לצד השלישי (הצד הסמוך) יש לנו שתי שיטות - באמצעות משפט פיתגורס או על ידי שימוש שוב בפונקציה SIN ב- Excel מזוויות אחרות.
על פי משפט פיתגורס, סכום הריבועים של שני הצדדים של המשולש הזוויתי שווה ערך לריבוע ההיפוטנוזה.
Hypotenuse2 = Opposite2 + צמוד 2
סמוך = (Hypotenuse2 - Opposite2) 1/2
ב- Excel נכתוב את זה כ,
= POWER ((POWER (Hypotenuse, 2) -POWER (Opposite, 2)), 1/2)
על ידי שימוש בנוסחה זו, אנו מחשבים את אורך הצד הסמוך
= POWER ((POWER (E2,2) -POWER (F2,2)), 1/2)
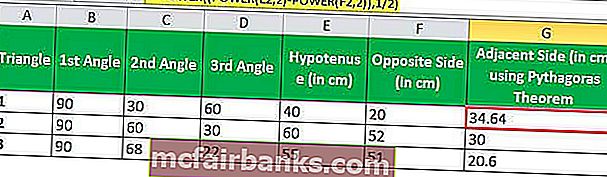
בשיטה השנייה אנו יכולים להשתמש ב- SINE של זווית 3 כדי לחשב את ערך הצד הסמוך
אם נסובב את המשולשים לכיוון 90 ° שמאלה, הצד הנגדי מוחלף עם הצד הסמוך ו- SIN של הזווית בין היפוטנוזה לצמוד יעזור לחישוב הערך של הצד השלישי.
= SIN (RADIANS (D2)) * E2

SIN ב- Excel דוגמה מס '2
יש בניין גבוה בגובה לא ידוע וקרן השמש בנקודת זמן יוצרת זווית בנקודה A של 75 מעלות, ובכך הופכת צל לבניין שאורכו 70 מטר. עלינו למצוא את גובה המגדל


גובה הבניין יחושב באמצעות פונקציית ה- SIN ב- Excel
SIN 75 ° = גובה הבניין / אורך הצללית בנקודה A.
לכן, גובה הבניין = SIN 75 ° * אורך הצללית בנקודה A.
לפיכך, גובה הבניין יהיה
= SIN (RADIANS (B3)) * B2

גובה הבניין הוא 67.61 מטר
SIN ב- Excel דוגמה 3
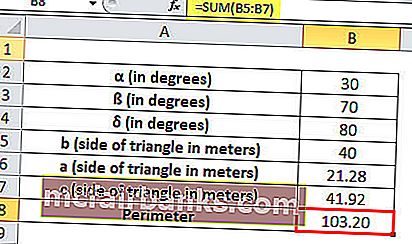
יש לנו ארץ בצורה של משולש, ששתי הזוויות שלה ניתנות כ- 30 ° ו- 70 ° ואנחנו יודעים רק את אורכו של צד אחד של המשולש שהוא 40 מטר. עלינו למצוא את אורך שלושת הצדדים האחרים ואת היקף המשולש.
עבור משולש, כאשר צד אחד וכל הזוויות ידועים אנו יכולים לחשב את הצדדים האחרים לפי כלל SINE
כלל סינוס בטריגונומטריה נותן יחס של זוויות חטא וצידי משולש על ידי נוסחת SIN
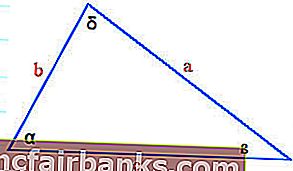
a / sin α = b / sin ß = c / sin δ
במקרה הזה,

α = 30 °, ß = 70 ° ו- δ = 180 ° - (30 ° + 70 °) = 80 ° וצד אחד של המשולש b = 40 מטר
כדי למצוא את הצדדים האחרים של המשולש נשתמש בכלל SINE
a = Sin α * (b / sin ß)
לָכֵן,
a = SIN (RADIANS (30)) * (B5 / SIN (RADIANS (70)))
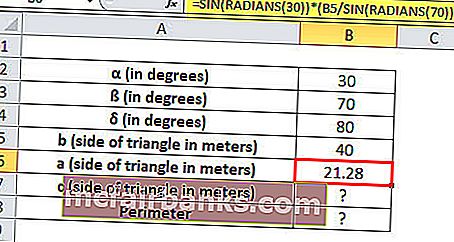
אורך הצד a = 21.28 מטר
באופן דומה, הצד השלישי c יהיה
c = Sin δ * (b / sin ß)
לָכֵן,
c = SIN (RADIANS (80)) * (B5 / SIN (RADIANS (70)))
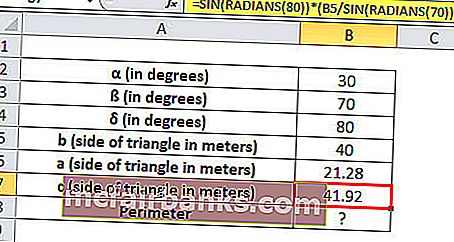
שלושת צלעות המשולש באורך 21.28, 40, 41.92 מטר.
היקף המשולש הוא סכום של כל הצדדים.
לכן ההיקף יהיה = SUM (B5: B7)