נוסחת רגרסיה מרובה | חישוב משוואת רגרסיה מרובה

מהי נוסחת רגרסיה מרובה?

נוסחת רגרסיה מרובה משמשת לניתוח הקשר בין משתנים תלויים למספר מרובים, והנוסחה מיוצגת על ידי המשוואה Y שווה לפלוס bX1 בתוספת cX2 בתוספת dX3 בתוספת E כאשר Y הוא משתנה תלוי, X1, X2, X3 הם משתנים עצמאיים , a הוא יירוט, b, c, d הם שיפועים, ו- E הוא ערך שיורי.

y = mx1 + mx2 + mx3 + b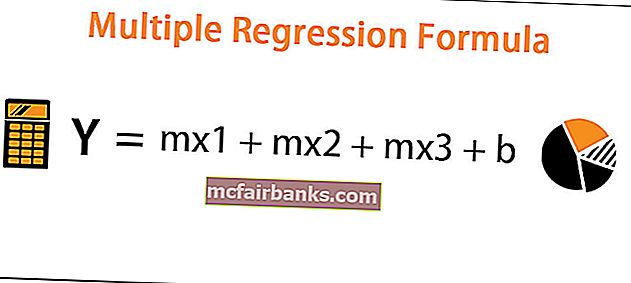

איפה,

• Y = המשתנה התלוי של הרגרסיה
• M = שיפוע הרגרסיה
• X1 = המשתנה העצמאי הראשון של הרגרסיה
• המשתנה x2 = המשתנה הבלתי תלוי השני של הרגרסיה
• המשתנה x3 = המשתנה העצמאי השלישי של הרגרסיה
• B = קבוע

הסבר על נוסחת ניתוח רגרסיה

רגרסיות מרובות הן שיטה לחיזוי המשתנה התלוי בעזרת שניים או יותר משתנים בלתי תלויים. תוך כדי ניתוח זה מטרתו העיקרית של החוקר היא לגלות את הקשר בין המשתנה התלוי למשתנים הבלתי תלויים. על מנת לחזות את המשתנה התלוי, נבחרים משתנים עצמאיים מרובים שיכולים לסייע בחיזוי המשתנה התלוי. משתמשים בו כאשר רגרסיה לינארית אינה מסוגלת לשרת את המטרה. ניתוח רגרסיה מסייע בתהליך האימות האם משתני המנבאים טובים מספיק בכדי לסייע בחיזוי המשתנה התלוי.

דוגמאות

אתה יכול להוריד תבנית Excel מרובת רגרסיה זו כאן - תבנית Excel מרובת רגרסיה

דוגמה מס '1

בואו ננסה להבין את הרעיון של ניתוח רגרסיות מרובות בעזרת דוגמה. בואו ננסה לברר מה הקשר בין המרחק שעבר נהג UBER לגיל הנהג לבין מספר שנות הניסיון של הנהג.

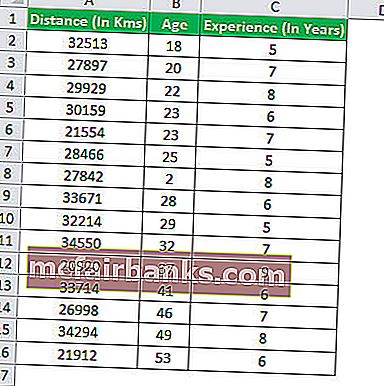
לחישוב של רגרסיה מרובה עבור לכרטיסייה נתונים ב- Excel ואז בחר באפשרות ניתוח הנתונים. להליך ולחישוב נוסף מתייחס למאמר הנתון כאן - ניתוח ToolPak ב- Excel

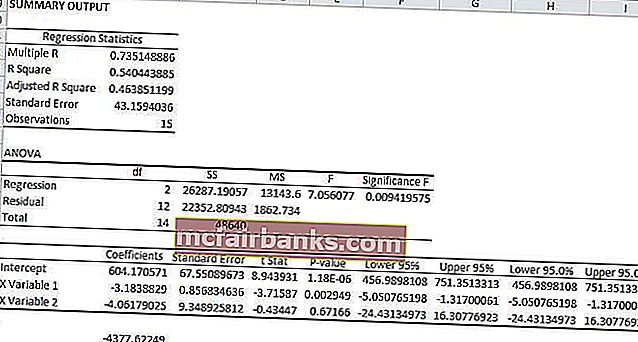
נוסחת הרגרסיה לדוגמא לעיל תהיה

1. y = MX + MX + b
2. y = 604.17 * -3.18 + 604.17 * -4.06 + 0
3. y = -4377

בדוגמה ספציפית זו, נראה איזה משתנה הוא המשתנה התלוי ואיזה משתנה הוא המשתנה הבלתי תלוי. המשתנה התלוי במשוואת רגרסיה זו הוא המרחק המכוסה על ידי נהג ה- UBER והמשתנים הבלתי תלויים הם גיל הנהג ומספר ההתנסויות שיש לו בנהיגה.

דוגמה מס '2

בואו ננסה להבין את הרעיון של ניתוח רגרסיות מרובות בעזרת דוגמה אחרת. בואו ננסה לברר מה הקשר בין ממוצע ציונים של כיתת סטודנטים לבין מספר שעות הלימוד וגובה התלמידים.

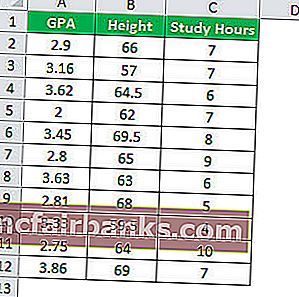
לצורך החישוב, עבור לכרטיסייה נתונים ב- excel ואז בחר באפשרות ניתוח הנתונים.

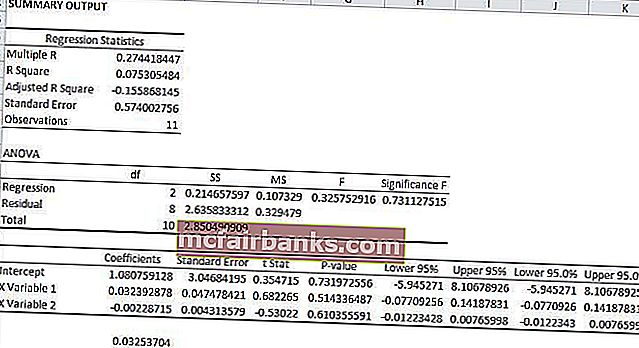
משוואת הרגרסיה לדוגמא לעיל תהיה

y = MX + MX + b

y = 1.08 * .03 + 1.08 * -. 002 + 0

y = .0325

 בדוגמה ספציפית זו, נראה איזה משתנה הוא המשתנה התלוי ואיזה משתנה הוא המשתנה הבלתי תלוי. המשתנה התלוי ברגרסיה זו הוא ה- GPA והמשתנים הבלתי תלויים הם שעות לימוד וגובה התלמידים.

דוגמה מס '3

בואו ננסה להבין את הרעיון של ניתוח רגרסיות מרובות בעזרת דוגמה אחרת. בואו ננסה לברר מה הקשר בין שכר קבוצת עובדים בארגון לבין מספר שנות הניסיון וגיל העובדים.

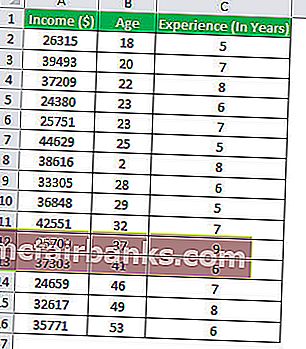
לצורך החישוב, עבור לכרטיסייה נתונים ב- excel ואז בחר באפשרות ניתוח הנתונים.

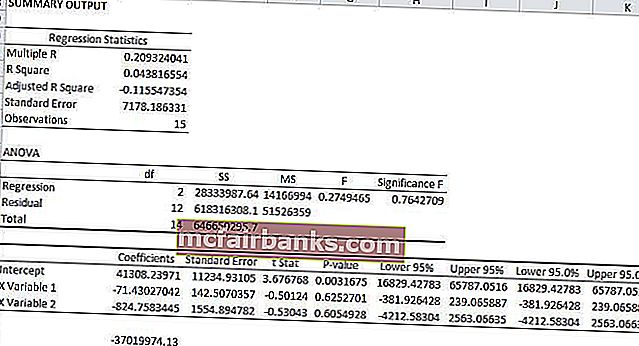
משוואת הרגרסיה לדוגמא לעיל תהיה

• y = MX + MX + b
• y = 41308 * .- 71 + 41308 * -824 + 0
• y = -37019

בדוגמה ספציפית זו, נראה איזה משתנה הוא המשתנה התלוי ואיזה משתנה הוא המשתנה הבלתי תלוי. המשתנה התלוי במשוואת רגרסיה זו הוא השכר והמשתנים הבלתי תלויים הם הניסיון והגיל של העובדים.

רלוונטיות ושימוש

רגרסיות מרובות היא שיטה סטטיסטית שימושית מאוד. רגרסיה משחקת תפקיד מאוד בעולם הפיננסים. הרבה חיזויים נעשים באמצעות ניתוח רגרסיה. לדוגמא, ניתן לחזות מראש מכירות של פלח מסוים בעזרת מדדים מקרו-כלכליים שיש להם מתאם טוב מאוד עם אותו פלח.